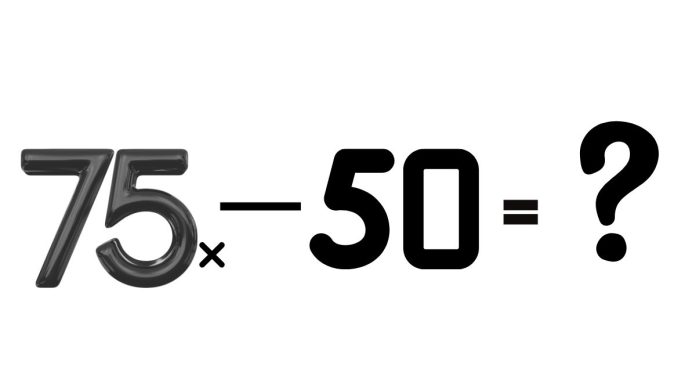What is the equivalent expression of 75x – 50?

In algebra, equivalent expressions are different mathematical expressions that represent the same value. The expression 75x – 50 can be rewritten in various forms that are equivalent but may appear different. Understanding how to simplify, factor, or manipulate an expression into its equivalent form is a fundamental skill in algebra. In this article, we’ll see how to find the equivalent expression of 75x – 50.

Breaking Down the Expression: 75x – 50

The expression 75x – 50 is a linear expression that involves two terms:

• 75x: A term where the variable x is multiplied by 75.
• -50: A constant term, with no variable attached.

Now, let’s look at the different ways we can rewrite this expression into an equivalent form.

1. Factoring the Expression

One of the most common methods for finding an equivalent expression is factoring. Factoring involves finding a common factor between the terms in the expression.

In 75x – 50, we can find the greatest common factor (GCF) of 75x and 50. The GCF of 75 and 50 is 25, so we can factor out 25 from both terms:

$$75x-50=25(3x-2)$$

Here, we’ve factored out 25, and the expression inside the parentheses is (3x – 2). This is an equivalent expression because when you expand it back, it results in the original form of 75x – 50.

2. Expanding the Factored Form

To verify that 25(3x – 2) is indeed equivalent to 75x – 50, you can expand it using the distributive property:

$$25(3x-2)=25\times 3x-25\times 2=75x-50$$

This shows that the factored form 25(3x – 2) is equivalent to the original expression 75x – 50. Expanding the factored expression brings us back to the same result, confirming the equivalence.

3. Expressing as a Sum of Terms

Another approach to writing an equivalent expression is to think of it as a sum of terms. For example, we could rewrite 75x – 50 as:

$$75x+(-50)$$

This simply expresses the subtraction of 50 as adding a negative number. While this might not seem like a huge transformation, it’s a valid equivalent form because the sum of the terms still equals 75x – 50.

4. Exploring the Use of Distributive Property

While the previous methods mainly focused on factoring, the distributive property can also be used to generate equivalent expressions in more complex situations. For instance, if we had a situation like 5(15x – 10), applying the distributive property could result in an equivalent expression.

In the case of 75x – 50, the distributive property is already shown when we factor it as 25(3x – 2) and expand it back out. Understanding how to apply distributive property principles helps to simplify or manipulate expressions when needed.

The expression 75x – 50 can be rewritten in various equivalent forms, with the most common and useful being the factored form:

$$75x-50=25(3x-2)$$

Both 75x – 50 and 25(3x – 2) represent the same mathematical relationship and will yield the same result when evaluated for any value of x. By factoring the expression, you have simplified it into a more compact form.

Recognizing and creating equivalent expressions is an important skill in algebra, helping to solve problems more efficiently, and in some cases, making complex expressions easier to work with. Whether factoring, expanding, or simply rearranging, these methods are essential tools for understanding and manipulating algebraic expressions.