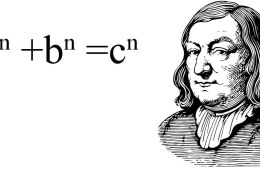Fermat’s Little Theorem is a principle in number theory that applies to prime numbers. It states that if you take any integer a that is not divisible by a prime number p, and raise a to a certain power, the result will always have a specific relationship when divided by p. More specifically, this relationship always leaves a remainder of 1.
In simple terms, it helps simplify calculations involving large exponents when working with prime numbers. This theorem is especially useful in areas like cryptography, where it can help in checking whether numbers are prime and simplifying calculations that would otherwise be very complex.