What Fraction Is Equivalent To 1/8?

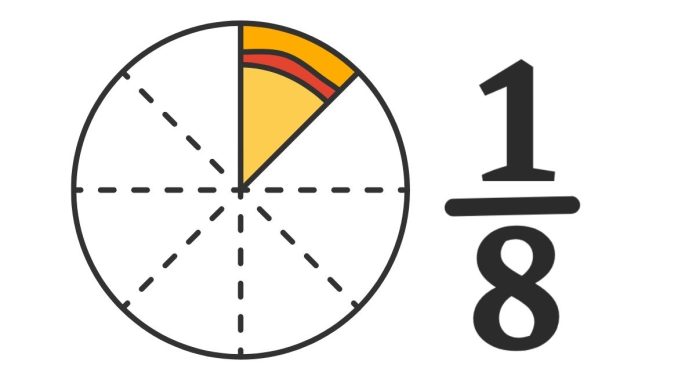
What does “equivalent fraction” mean?

Two fractions are equivalent if they represent the same value or proportion. This can be achieved by multiplying or dividing both the numerator (top number) and the denominator (bottom number) by the same non-zero number.

 How do we find equivalent fractions for 18\frac{1}{8}?

To find an equivalent fraction to 18\frac{1}{8}, we need to multiply both the numerator and the denominator by the same non-zero integer.

Example 1: Multiply both by 2

• Multiply the numerator (1) by 2: $=2$
• Multiply the denominator (8) by 2: $=16$

So, we get the equivalent fraction 216\frac{2}{16}.

Example 2: Multiply both by 3

• Multiply the numerator (1) by 3: $=3$
• Multiply the denominator (8) by 3: $=24$

So, we get the equivalent fraction 324\frac{3}{24}.

Example 3: Multiply both by 4

• Multiply the numerator (1) by 4: $=4$
• Multiply the denominator (8) by 4: $=32$

So, we get the equivalent fraction 432\frac{4}{32}.

Example 4: Multiply both by 5

• Multiply the numerator (1) by 5: $=5$
• Multiply the denominator (8) by 5: $=40$

So, we get the equivalent fraction 540\frac{5}{40}.

Verifying the fractions

To verify that all these fractions are equivalent to 18\frac{1}{8}, we can divide the numerator by the denominator for each fraction and check that they all equal 0.125:

• 18=0.125\frac{1}{8} = 0.125
• 216=2÷16=0.125\frac{2}{16} = 2 \div 16 = 0.125
• 324=3÷24=0.125\frac{3}{24} = 3 \div 24 = 0.125
• 432=4÷32=0.125\frac{4}{32} = 4 \div 32 = 0.125
• 540=5÷40=0.125\frac{5}{40} = 5 \div 40 = 0.125

Since all the fractions simplify to the same value (0.125), we can confirm they are indeed equivalent.

Conclusion

Therefore, the fractions 216,324,432,540\frac{2}{16}, \frac{3}{24}, \frac{4}{32}, \frac{5}{40}, and so on, are all equivalent to 18\frac{1}{8}. These fractions represent the same value, but they have different numerators and denominators.