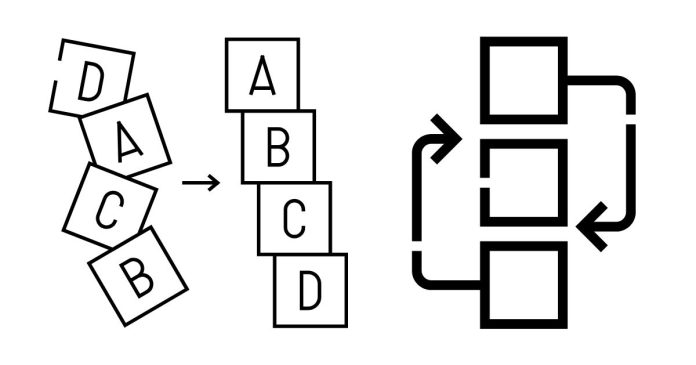
Sorting Algorithms

Sorting algorithms are methods used to arrange data in a specific order, typically ascending or descending. They are fundamental in computer science and are used in various applications, such as searching, organizing, and optimizing data.

Types of Sorting Algorithms

1. Comparison-Based Sorting Algorithms These algorithms compare elements to determine their order.
   • Bubble Sort
   • Selection Sort
   • Insertion Sort
   • Merge Sort
   • Quick Sort
   • Heap Sort
2. Non-Comparison-Based Sorting Algorithms These algorithms use methods other than comparisons, often with constraints on the data.
   • Counting Sort
   • Radix Sort
   • Bucket Sort

Popular Sorting Algorithms

1. Bubble Sort

• Description: Repeatedly swaps adjacent elements if they are in the wrong order.
• Time Complexity:
  • Best Case: $O(n)$
  • Worst Case: O(n2)O(n^2)O(n2)
• Usage: Simple but inefficient for large datasets.

2. Selection Sort

• Description: Finds the smallest element and places it at the beginning, then repeats for the remaining elements.
• Time Complexity:
  • Best Case: O(n2)O(n^2)O(n2)
  • Worst Case: O(n2)O(n^2)O(n2)
• Usage: Easy to implement but inefficient.

3. Insertion Sort

• Description: Builds a sorted list by repeatedly taking an element and inserting it into its correct position.
• Time Complexity:
  • Best Case: $O(n)$
  • Worst Case: O(n2)O(n^2)O(n2)
• Usage: Efficient for small or partially sorted datasets.

4. Merge Sort

• Description: Divides the array into halves, sorts each half, and merges them.
• Time Complexity:
  • Best Case: $O(n\log n)$
  • Worst Case: $O(n\log n)$
• Usage: Stable and efficient for large datasets.

5. Quick Sort

• Description: Uses a pivot element to partition the array into two subarrays and recursively sorts them.
• Time Complexity:
  • Best Case: $O(n\log n)$
  • Worst Case: O(n2)O(n^2)O(n2) (rare with proper pivot selection)
• Usage: Preferred for large datasets due to its average-case efficiency.