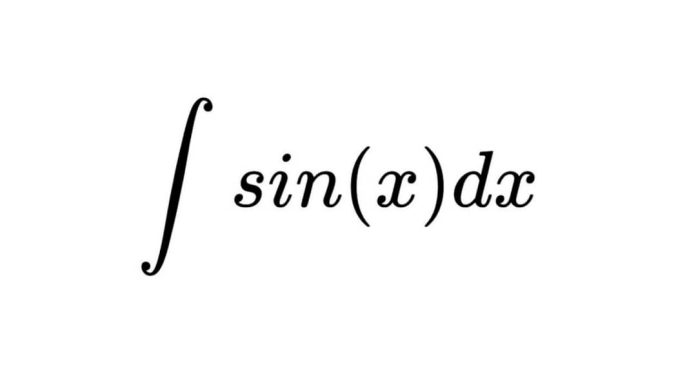Integration of Sin X – Formula, Derivation and Graph

Overview of the integration of sin(x):

Formula:

∫sin(x) dx = -cos(x) + C

where C is the constant of integration.

Derivation:

To derive this formula, we can use the definition of integration as the antiderivative of a function. We know that the derivative of cos(x) is -sin(x), so we can write:

d(cos(x))/dx = -sin(x)

Now, we can integrate both sides with respect to x:

∫d(cos(x)) = ∫-sin(x) dx

cos(x) = -∫sin(x) dx

Now, we can multiply both sides by -1 to get:

∫sin(x) dx = -cos(x) + C

Graph:

The graph of ∫sin(x) dx = -cos(x) + C is a cosine curve that has been reflected about the x-axis and shifted vertically by the constant C.

Key features of the graph include:

– Amplitude: 1
– Period: 2π
– Phase shift: 0 (without the constant C)
– Vertical shift: C

Note that the graph of ∫sin(x) dx is not the same as the graph of sin(x). The integral of sin(x) is a cosine curve, while the graph of sin(x) is a sine curve.