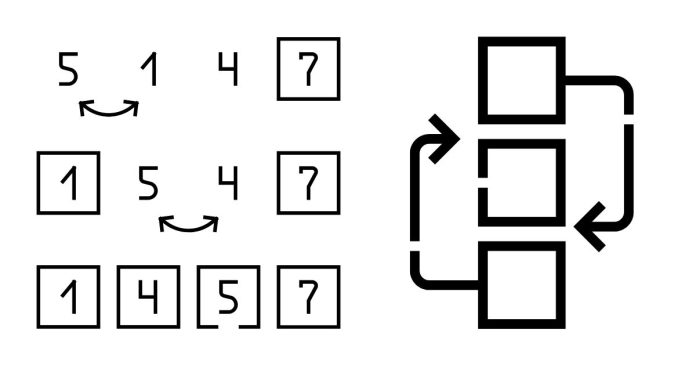
Insertion of Sort Algorithm

Insertion Sort is a simple and intuitive sorting algorithm that works similarly to the way you might sort playing cards in your hand. The algorithm builds the final sorted array one element at a time by comparing and inserting elements into their correct position.

How It Works

The array is conceptually divided into two parts:

1. Sorted Part: Initially contains the first element.
2. Unsorted Part: Contains the remaining elements.

The algorithm iteratively picks elements from the unsorted part and inserts them into their correct position in the sorted part.

Algorithm Steps

1. Start with the second element (index 1) in the array as the key.
2. Compare the key with elements in the sorted part (elements before the key).
3. Shift all elements in the sorted part that are greater than the key to the right by one position.
4. Insert the key into its correct position.
5. Repeat this process for all elements in the unsorted part.

Pseudocode

for i = 1 to n-1:
    key = array[i]
    j = i - 1
    while j >= 0 and array[j] > key:
        array[j + 1] = array[j]
        j = j - 1
    array[j + 1] = key

Example

Input: [8, 4, 3, 7, 2]

1. Initial Array: [8, 4, 3, 7, 2]
2. Step 1 (Key = 4): Compare 4 with 8. Shift 8 to the right and insert 4.
   Result: [4, 8, 3, 7, 2]
3. Step 2 (Key = 3): Compare 3 with 8 and 4. Shift both 8 and 4 to the right and insert 3.
   Result: [3, 4, 8, 7, 2]
4. Step 3 (Key = 7): Compare 7 with 8. Shift 8 to the right and insert 7.
   Result: [3, 4, 7, 8, 2]
5. Step 4 (Key = 2): Compare 2 with all elements. Shift 8, 7, 4, and 3 to the right and insert 2.
   Result: [2, 3, 4, 7, 8]

Time Complexity

• Best Case: O(n) (Already sorted array, no shifting needed).
• Worst Case: O(n²) (Reversed array, maximum shifts needed).
• Average Case: O(n²).

Space Complexity

• Space: O(1) (In-place sorting, no additional memory required).

Advantages

1. Simple and easy to implement.
2. Efficient for small or nearly sorted arrays.
3. Stable sorting algorithm (does not change the relative order of equal elements).

Disadvantages

1. Not suitable for large datasets due to its quadratic time complexity.
2. Performs poorly on reverse-ordered or large unsorted arrays.

Python Implementation

def insertion_sort(array):
    for i in range(1, len(array)):
        key = array[i]
        j = i - 1
        # Shift elements of the sorted part that are greater than the key
        while j >= 0 and array[j] > key:
            array[j + 1] = array[j]
            j -= 1
        # Insert the key into its correct position
        array[j + 1] = key

# Example Usage
arr = [8, 4, 3, 7, 2]
insertion_sort(arr)
print("Sorted Array:", arr)

Output

For the example [8, 4, 3, 7, 2], the sorted array will be:

Sorted Array: [2, 3, 4, 7, 8]