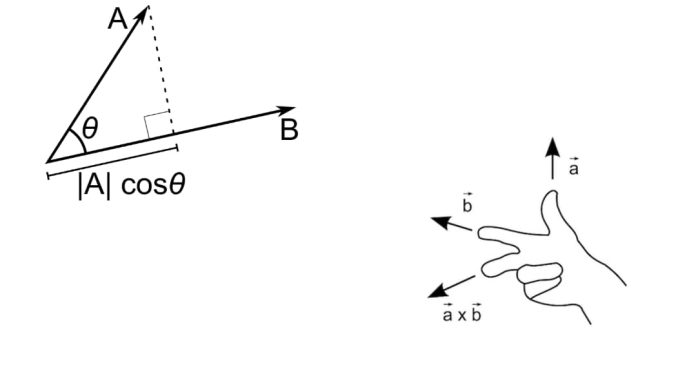
The dot product and cross product are two operations performed on vectors in mathematics and physics.
1. Dot Product: The dot product (or scalar product) of two vectors results in a scalar (real number). It is calculated by multiplying the corresponding components of the vectors and summing the results. Mathematically, for vectors A = (A₁, A₂, A₃) and B = (B₁, B₂, B₃), the dot product is:
A · B = A₁B₁ + A₂B₂ + A₃B₃.
The dot product measures the similarity or projection of one vector onto another and is zero if the vectors are perpendicular.
2. Cross Product: The cross product (or vector product) of two vectors results in another vector. This vector is perpendicular to both original vectors and has a magnitude equal to the area of the parallelogram formed by them. The formula for the cross product of vectors A and B is:
A × B = |A| |B| sin(θ) n,
where θ is the angle between the vectors, and n is a unit vector perpendicular to the plane containing A and B